このまえHな講義*1を受けてたあとに、@polamjag 氏とダベってたら 「音割れ音源復元できないか」 みたいな話がでて面白そうだったので趣味研究してみた成果だったりします。
信号解析初経験な上に片手間でやった研究なので、かなり穴だらけだと思うのでお気づきのことがありましたら、ご指摘お願いします。

背景

話によると、そこらへんで買った音源って音割れしてるらしい。
audacityで[view]->[show clipping]をオンにすると音割れ箇所を可視化してくれる。

ノーポイッを見てみた図。
(amazon mp3で購入、買ってない方ぜひ買いましょう。 http://www.amazon.co.jp/dp/B017BAK632 )

f:id:cocu_628496:20160206025240p:plain

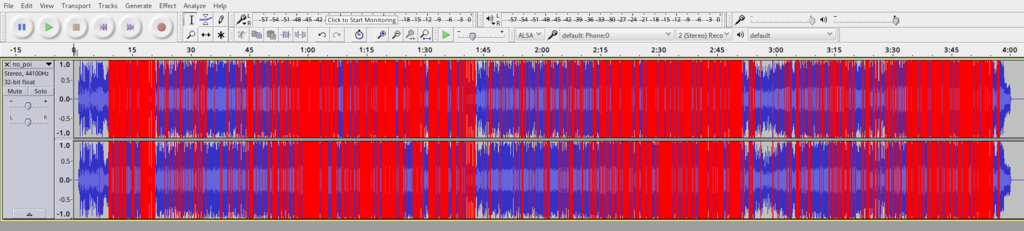
あかい。。。
ということで、ｻｰﾍﾞｲするこくたんであった。

目的

音割れしている音源(5分ぐらいの)をいい感じに補完して 人間の耳にやさしく 補完する。
途中で紹介する論文を実際に実装して declipper界隈がどんな雰囲気なのか知る

音割れとその性質

音割れとは、ある上下限で波形が切れちゃってる状態です。
音割れすると周波数スペクトルがスパースじゃなくなる性質を利用します。

適当に例を示すと、140Hzと300Hzと500Hzの音を合成したものがあるとして。

f:id:cocu_628496:20160206032453p:plain

%matplotlib inline
n=44100
t = np.linspace(0,0.05,num=n)

s = 1.2*np.sin(2*np.pi*145*t)+0.8*np.sin(2*np.pi*300*t-np.pi/4)+0.5*np.sin(2*np.pi*500*t-np.pi/3)
plt.plot(x,s)
plt.ylim(-3,3)
plt.savefig('fig/raw_wave.png')

周波数スペクトルを見てみると、ちゃんと140Hzと300Hzと500Hzあたりにたってあす。
だいたいスパースになってます。

f:id:cocu_628496:20160206032505p:plain

plt.plot(np.fft.fftfreq(n,0.05/n),np.abs(np.fft.fft(s, n)))
plt.xlim(-1,2000)
plt.savefig('fig/raw_spec.png')

音割れを発生させるために、上下限でclipします。このとき、あるしきい値より大きいものはしきい値に、しきい値より小さいものは負のしきい値になっていることに注目してください。

f:id:cocu_628496:20160206032607p:plain

s_clipped = np.clip(s,-1,1)
plt.plot(x,s, label="raw")
plt.plot(x,s_clipped, label="clipped")
plt.legend()
plt.ylim(-3,3)
plt.savefig('fig/clipped_wave.png')

周波数スペクトルを見ると崩れてます。
ここで、比較的高周波のところにきてます。
さっきよりスパースじゃなくなってます。

f:id:cocu_628496:20160206032705p:plain

plt.plot(np.fft.fftfreq(n,0.05/n),np.abs(np.fft.fft(s, n)), label="raw")
plt.plot(np.fft.fftfreq(n,0.05/n),np.abs(np.fft.fft(s_clipped, n)), label="clipped")
plt.xlim(-1,2000)
plt.savefig('fig/clipped_spec.png')

以上の性質より、音割れ前の音声は周波数スペクトルがスパースであると仮定します。

実際に聴いてみるとよくわかります。

元音源

http://2016.typowriter.org/declipping_0208/raw_wave.ogg

音割れしてるやつ

http://2016.typowriter.org/declipping_0208/clipped_wave.ogg

今日の論文

今回はSiedenburg氏の論文を基本的にとりあげつつ進めます。とりあえず、偉大なる先人がどのように考えたかを実際に実装してみます。

Kai Siedenburg, Matthieu Kowalski, Monika Dorer. AUDIO DECLIPPING WITH SOCIALSPARSITY. ICASSP 2014, May 2014, Florence, Italy. pp.AASP-L2, 2014. <hal-01002998>

ICASSP 2014の論文です。ieee xploreが出てくるんですが、フランスのpublisherのHALから同じ論文が無料でとれるっぽい。
(ちょこちょこミスが多い気がするので、ICASSPに投げる前のdraftをHALになげたような気が…)

https://hal.archives-ouvertes.fr/hal-01002998/document

超要約

周波数スペクトルがスパースになるように推定する
- →周波数スペクトル推定問題に帰着
- 入力値を周波数スペクトルに変換する行列が必要
  - 短時間フーリエ変換する行列gabor frameを用いる*2
- gabor frameと周波数スペクトルは複素数になることに注意
スパース推定問題を制約付き0ノルム最小化問題で定式化する
- 0ノルムだと解けないので緩和する
  - 二乗誤差 + 二乗ヒンジ + lasso
上記式の最小化問題は近接勾配法で求解可能
- 加速勾配法も使う
- いいかんじのproximal operatorを使うと精度が上がる(謎)

定式化

入力値に関して

音割れしている波形: $\mathbf{y}\in\RealSet^{T}$
$\mathbf{y}$のうち音割れしていない(reliable)部分: $\mathbf{y}^r\in\RealSet^{M}$, ただし$M\leq T$
- $\mathbf{y}^r = {M}^r \mathbf{y}$
- 音割れしていないものを抽出する単位行列を潰した行列 $M^{r}\in\BinarySet^{M \times T}$
音割れしている(clipped)値: $\Theta^\text{clip}\in\RealSet^{T-M}$
- $\Theta^\text{clip} = {M}^c \mathbf{y}$
- 音割れしているものを抽出する単位行列を潰した行列 $M^{c}\in\BinarySet^{(T-M) \times T}$
- $\Theta^\text{clip}$の要素は$\pm\theta^\text{clip}$となります。

ここまでは、単純にnotationしているだけ。

周波数スペクトル絡み

推定した波形 $\hat{\vec{y}}\in\RealSet^{T}$(論文中にはないが便宜上置いた)
- $\vec{\hat{y}} = \Phi\alpha$
周波数スペクトル $\mathbf{\alpha}\in\ComplexSet^{N}$
- sparseと仮定
time-frequency dictoinary $\Phi\in\ComplexSet^{T\times N}$
- 列ベクトルがある時間点1つの周波数になっている行列
- $\Phi \alpha$ は istft(a)とおなじ
short time fourier transform: $\Phi^{\ast}\in\ComplexSet^{N\times T}$
- $\Phi^{\ast}\vec{y}\simeq c\alpha$という認識でよいはず。
- time-frequency dictionaryの随伴行列(転地+複素共役)
- tightなframeだと$\Phi\Phi^{\ast}=c\mat{I}$ ($c$は正の定数)、となるらしい。(よくわからない)
- $\Phi^{\ast} \vec{y}$ は stft(y)とおなじ

最適化問題への変換

考えられる制約条件は以下の3つ

音割れしていない部分は、真の音源 と 音割れ音源が同じ
- $||y^{r} - M^{r}\vec{\hat{y}}||^{2}_{2}\leq \epsilon$みたいに小さい$\epsilon$で抑えられるはず
音割れしている部分は、絶対値で比べると 真の音源 は 音割れ音源 より大きい
- 音割れしている部分は上下限で区切られているため、絶対値で比較すると 音割れしていない値 より小さい値になっている。
- 下図のオレンジ線のようにはならない、必ず緑線のようになる。
- $|M^{c}\Phi\alpha|\geq|\Theta^\text{clip}|$

f:id:cocu_628496:20160229090027p:plain

以上より、問題は上記制約を満たしかつ以下の最小化問題となる。

$$ \hat{\alpha}=\argmin[\alpha]{~||\alpha||_0} $$

緩和

でもこれは解けないので

制約$||y^{r} - M^{r}\hat{y}||^{2}_{2}\leq \epsilon$ をそのまま二乗損失に
制約$|M^{c}\Phi\alpha|\geq|\Theta^\text{clip}|$ を二乗ヒンジ損失に
- しきい値$\pm\theta^{clip}$より 絶対値 で小さいときに損失を加えたいので場合分けしている
目的関数$||\alpha||_0$をLasso項にする

f:id:cocu_628496:20160229225004p:plain

短時間フーリエ変換

フーリエ変換は$-\infty, \infty$の積分と全区間なので、ある時間点近傍での周波数がわかりません。
なので、窓関数を掛けてある時間点あたりの周波数を出します。

今回つかうhanning窓はこんな形で、畳込み関数みたいにカクカクじゃないです。

f:id:cocu_628496:20160228155609p:plain

pythonのライブラリ転がっていなかったので、とりあえず、こんな感じに実装。
あんまりあってる自信ないですが、短時間フーリエ変換して逆変換掛けたときの誤差の合計が(ノーポイッの7秒間の音源で)$10^{-4}$ぐらいになったのでまぁこれでいいかなと

stft.py · GitHub

私は信号解析全く詳しくないのですが、自習する上でこの資料がよかったです。

http://hil.t.u-tokyo.ac.jp/~kameoka/SAP/Kameoka2011Speech_and_Audio_Processing05.pdf

近接勾配法

$L_1$ノルムのような、微分不可能な項と最適化手法です。
勾配法で更新するときに 「スパースになるようにちょっと動かす」 処理をします。
書くと結構大変なので省略します。この青い本がよかったです。

確率的最適化 (機械学習プロフェッショナルシリーズ)

作者: 鈴木大慈
出版社/メーカー: 講談社
発売日: 2015/08/08
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

近接勾配法を$L_1$ に特殊化したISTAですが、ネット上ならこの資料がよかったです。
この論文では、 $L_1$ ノルムのみなのでISTAとその高速化であるFISTAを使っています。
私は近接勾配法を劣勾配ることしかしらなかったのでメジャライザー最適化あたりは勉強になりました。

http://www-adsys.sys.i.kyoto-u.ac.jp/mohzeki/Presentation/lectureslide20150902-3.pdf

http://www-adsys.sys.i.kyoto-u.ac.jp/mohzeki/Presentation/lecturenote20150909.pdf

http://imi.kyushu-u.ac.jp/~waki/ws2013/slide/suzuki.pdf

論文ではproximal opetaorを4つ考えています。
lassoとempirical wiener、近接時間において同一周波数が似るであろうからgroup lassoにした window group lassoと同様にgroup版の persistent empirical wienerです。
empirical wienerを $L_1$最適化の文脈でつかうのは大丈夫なのか…?とちょっと思いましたが、信号解析界隈だとISTAと一緒によく使っているようです。

f:id:cocu_628496:20160229220238p:plain

実装

ごりごりっと。
論文中のアルゴリズムがISTAと言いつつFISTAだったり、$\gamma$が固定で書いてあって、そのままだと発散してしまったので、ちょっと変えてあります。
この実装では、極々稀にlossが単調減少しなかったり、たぶんどこかの実装が悪いと思うので参考にしないでください。
たぶん複素あたりとかで絶対値付け忘れてるとか。あと収束条件も適当にiterator countで決めてるので。

social_sparcity.ipynb · GitHub